来看几个名词
半平面:我们画一个2d坐标轴,好我们有了一个平面。然后我们画一条线,分出来的这两部分就叫半平面啦。
凸多边形:就是这个多边形(在二维空间里),是个凸包。
多边形的核:在一个多边形里(任意样子的多边形,可以不是凸多边形),找到一个区域,站在这个区域里的任意位置,都能看到所有多边形顶点。这个区域就叫核。
求二维平面里,由不等式约束的区域
题意描述:给出若干个形如$Ax+By+C>=0$的不等式(显然每个不等式在坐标系里面可以表示为一片区域),求由这些不等式围出的区域。
输出:围成这个区域用了几个不等式,分别是哪几个(逆时针顺序输出)?
建议先粗略的看一下这个 讲的很好 大受启发!https://blog.csdn.net/zuzhiang/article/details/78395670
朴素算法就是:求出所有交点,再保留合法的的点。费时费力不能这样,看下面这个机智的算法。。
然后我们详细展开一下
- 每个不等式相当于 把无限大的平面切上一刀,保留一半的区域。
- 我们求的结果就是不等式的交集,换句话说 切上若干刀,剩下的部分。
- 想象成把一块方木头一刀一刀砍成圆木头。
- 剩下的结果可以是“无限空间”,也可以是“有限空间”,也可以是“无解”。
- 我们把每个不等式想象成“有方向的直线”,直线左侧为切一刀以后的保留部分。
- 下面讲到的算法是:逆时针方向削切平面。

(推荐一个画图网站 https://www.geogebra.org/classic)
先把所有的有向直线(不等式)按顺序排好,下文按逆时针:指向西南的->正南的->东南的->正东的...
然后按照这个顺序把每根线拿出来切削平面,扔掉右半平面,保留左平面。
规定 struct Line 表示一条直线,
我们用双端队列 deque<Line> ans; 存这题的答案。
使用 array<Line> L; 存排好序的线。
(先不考虑 有方向相同的两根直线 的情况)
首先ans里先放进去L[0]第一根。
重要提示:这条线和当前这个“待切削的毛胚”无穷远处有两个交点。
我们发现:每引入一根线,总会与ans里面的线有交点。
放了若干根黑线以后如下图
(下图是引自参考blog里面)蓝色为待处理的一根线,且还没有插入ans里面,黑色的线已经在ans里面了。
在这个算法中,我们认为ans.first()的开头和“圆胚无限远处”相交,ans.last()的结尾与“圆胚无限远处”相交。(即图中那个空槽)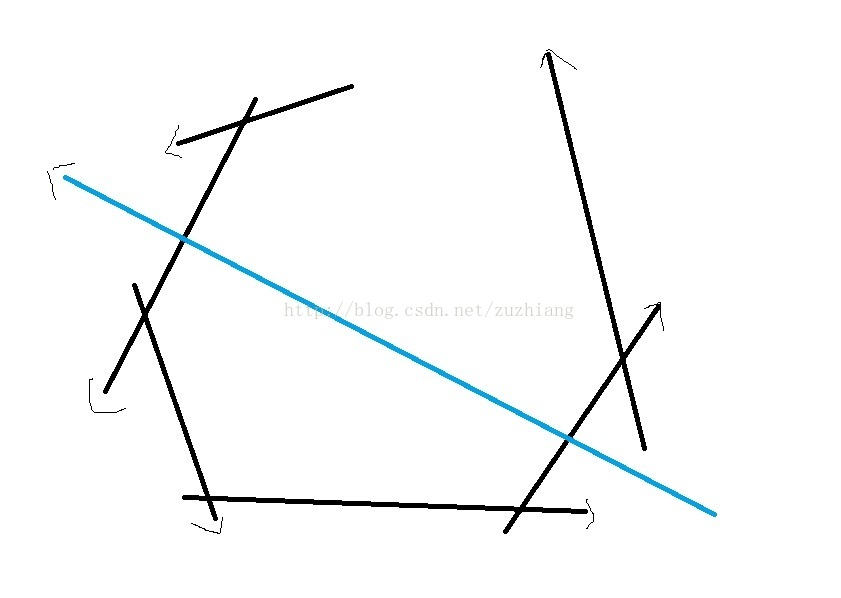
由于这条线的引入,使得ans里存的“第一条线”以及“最后一条线”没意义了(范围重复了,新的线描述的范围更小)。因此我们弹出ans里面第一根Line,以及最后一根Line。(线没了交点自然就没了)
如何判断这无意义了:被弹出的线的交点在这条新线的右边。每条线分别有两个交点,例如ans.first()的交点是“两黑线交点”和“圆胚无限远处”。
【补充】如何理解线从ans里面弹出来?“新线”迫使“旧线交点”在新线右侧,说明“旧线”的切割功能被“新线”完全替代了。
我们发现ans里面的线+待插入的蓝线,按顺序组成了答案,相邻两条线有交点,但是ans.front()和ans.back()是否相交我们不关心。
【到这里暂停⏸️ 引导一下思想】
- 想像一个无限大的不规则形状胚,每个不等式代表切一刀,并扔掉一部分。
- 逆时针顺序开始削切,想象成把一块方木头一刀一刀砍成圆木头。
- 无解就是 这刀切完以后,材料全扔了。
- 有无穷解就是 全切完了,还有开口。
【重要】请再次思考,以什么准则判定无解?
答案:我们认为,有解=有交点在“新的一刀”右边,无解=这条新线右边没有交点。
(包括无穷远处的交点)有交点 和 切完还有可用材料 是一样的啊!
换句话说,因为线排过序了,L中剩余的线一定落在ans.front()和ans.back()之间的角度里:我们不能画出一条有用的切割(切料 不是切空气),让所有已知交点都在这条线的右边。(包括无穷远边界交点)
然后我们把蓝色的线放入ans末尾...
此时ans里面有:{四条黑色的线、一条蓝色的线}
因此ans里面有6个交点:四个图中可见的交点,两个无穷远处交点
注意:把线放到ans.back(),我们不认为ans.front()和蓝色的线有交点。图中用白点表示此交点暂不考虑
我们放入这根蓝色的线时候发现,因为我们放线是按逆时针顺序放的,
因此“ans.back()和无穷远处的交点”必然被切割掉了,因此不用判断,只需要判断“ans.back()交ans.backback()”和新线的关系即可。
同理若“ans.front()和ans.second()交点”如果被切割掉了,那么"ans.front()和无穷远的交点"也不用判,必然也被切掉了。
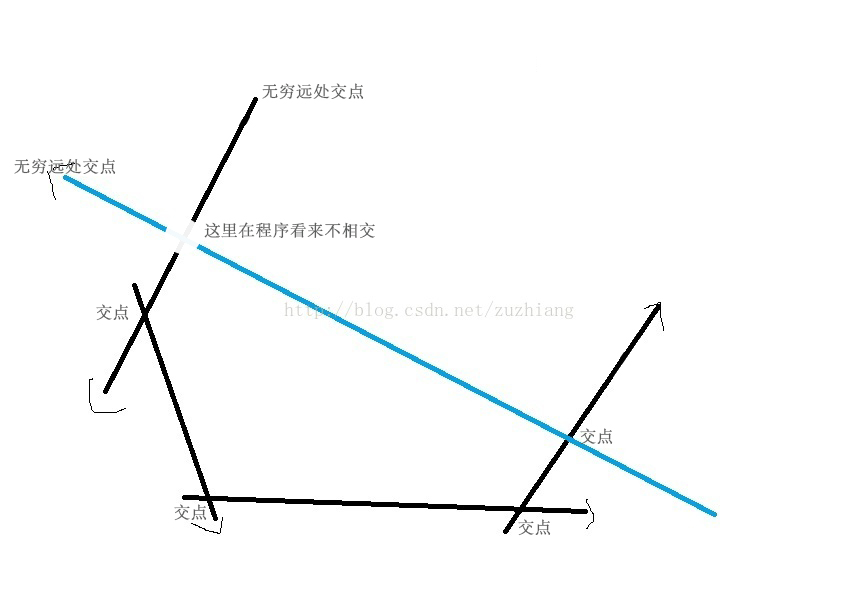
每次添加新线都要维护ans,在新线入ans之前,若ans里面的线没有交点了(包括无穷远处交点),说明无解。因此“关于无穷远交点的判断”只在此用了。
接下来看一个特例 处理绿色的线
又放进去两根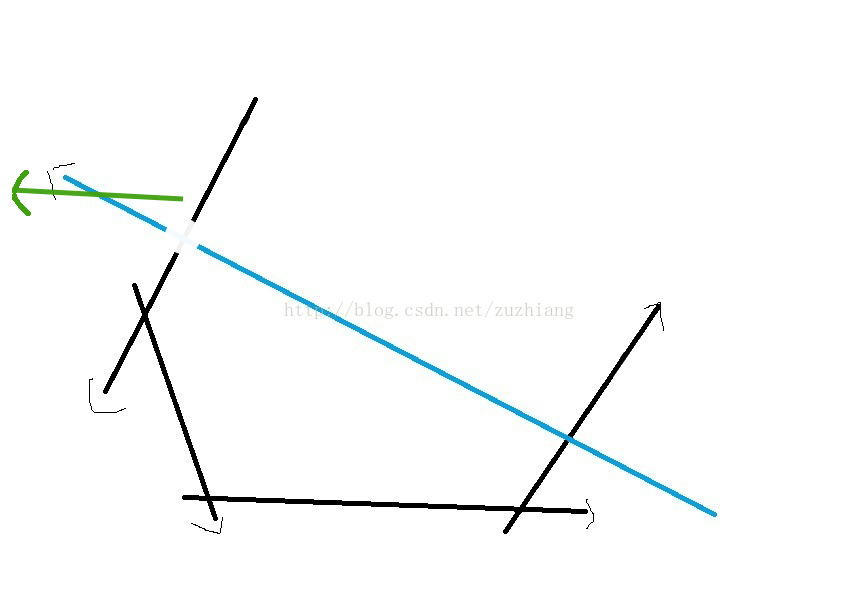
由上文原则(ans里面的交点都在新线左边)可得,绿线应该合理合法的放进ans。
但是从图里看来不应该放进去啊?
问题出在这里:
我们刚开始把线都逆时针排了序,这保证了:每次放入的一根线都能截断“ans的尾部的那根线”,从而更新现有解。
想象这样一个物件,一些木条代表上面的线,相交点钉上钉子可以自由旋转活动。这就是在算法角度上看到的东西,算法不关注角度和长度到底是多少,他们只关注这些木条(ans队列)是按照这个顺序排的,表示成木条首尾相接。当我们试图展开和收缩手里这个玩具时,这个问题就再现了。
所以站在死板的算法的角度上来说,我们没法预估到“新线”和“ans.front()这根线”的关系:新线没插入ans之前和ans.back()的交点 可能已经越过了ans.front(),导致了“新线”包围在了ans已知解的外面。(如下图)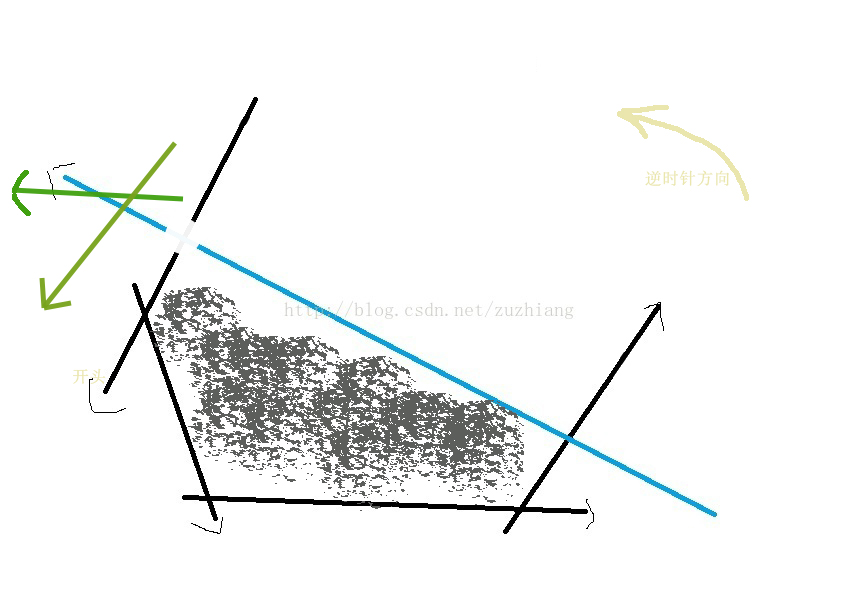
两个绿线是最后插入的,这两个绿线对可行解(阴影部分)已经构成了包围之势,因此舍掉他们的理由是:ans里面最后三根线,(只看相邻的线)构成的两个交点为{绿&绿}{深绿&蓝},这两个交点在ans.front()这跟开头的线的 右侧。
最后,若出现方向相同的两个直线
其实不用考虑,方向相同时候额外判断一下,保留最靠“内侧”的那根。
见代码吧