从简单的入手,在网上看了许多许多教程,有些疑问记下来。。
学以致用,从一道题开始 pku2976。
引入一个还不错的教程http://jcf94.com/2014/11/04/2014-11-04-POJ-2976/
01分数规划与单调性的理解 推理单调性
以上面那个题举例,按照推倒,先设函数 F = (a1 - x*b1) + (a2 - x*b2) ..... ,然后我们把每一项提出来,变成这个式子: y = (a - bx) 然后我们画线吧,如下图,交y轴于y=a,交x轴于x=a/b。
我们现在题目要求要舍掉k条线,所有线都在图上画出来了。
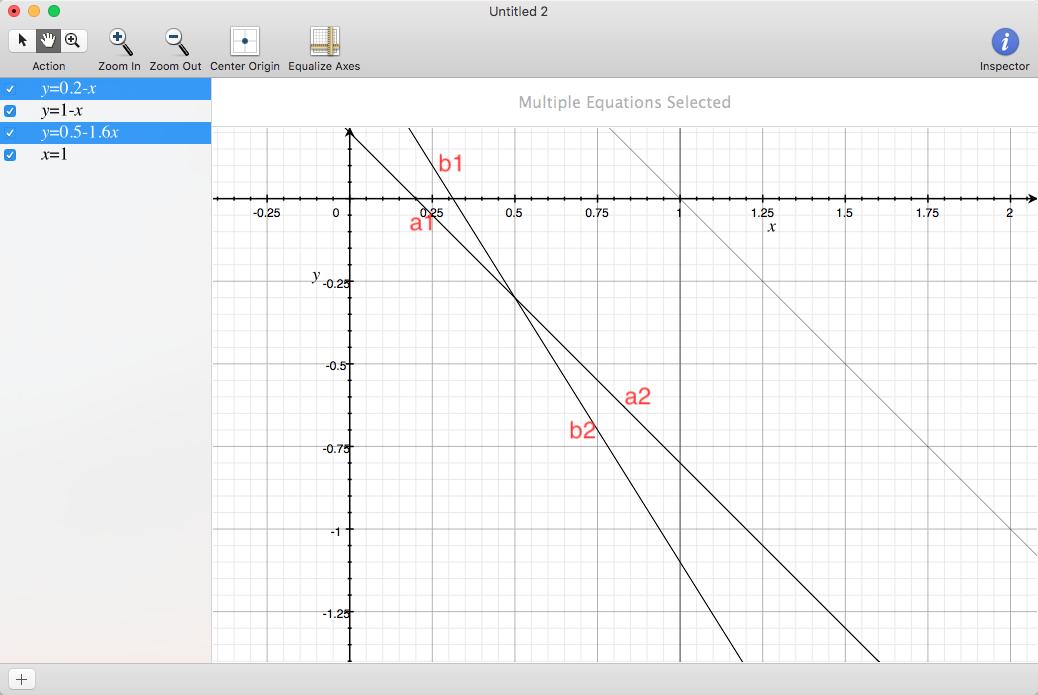
这个图我们列举了两条线,线a,线b(和上面的a,b参数无关,我就随手起了个名字。)
我们把所有的线都画在图上,然后从x=0一直走到x=1,会发现每一条线都是单调递减的。
这三条线,我们关注x=0,x=0.5,x=1的三个交点,把整个图分为两部分,(0->0.5)&&(0.5->1)。
我们的做法是:针对每段贪心,舍掉k条y最小的线段。
可以发现我们舍掉的是整个图的最底下的包裹线(下凸包):即a1&b2。
每段指的是:两个交点中间的一段没有交点的部分。
现在我们证明:在每段,按照贪心(舍掉k个最小值),F函数依然是单调递减的函数。
这个成立,才能二分答案。
下面我们假设舍掉k=1颗线。
已知b1 > a1 > a2 > b2。
在(0->0.5)段,按我们的做法会去掉a1,而经过交点,我们选了剔除b2并保留a2。
这样理解:b1与a2组合成一条线,发现这条线依然保持单调递减。
因此得到:用我们的方法选线,F过焦点前后保持单调递减的。
扩展:如果在x=0.5处有不止一条条线出现交点,而且k>1。
假设交点之前要剔除的线组成了{线集合M},经过交点以后,有一部分{线集合N}替换掉了{M}里面的一些线。
{集合N}在交点前是被保留的。
因此我们有一个差不多的结论:{N}在交点前的线们,与在交点后“被{N}从{M}里置换出来的一部分线”,一对一组成了新线,这些新线均保持单调递减。
补充原因:如果相交,必然{N}这部分线会跑到被顶替的线的下面。(见上图)
最后,再给一个图供大家推理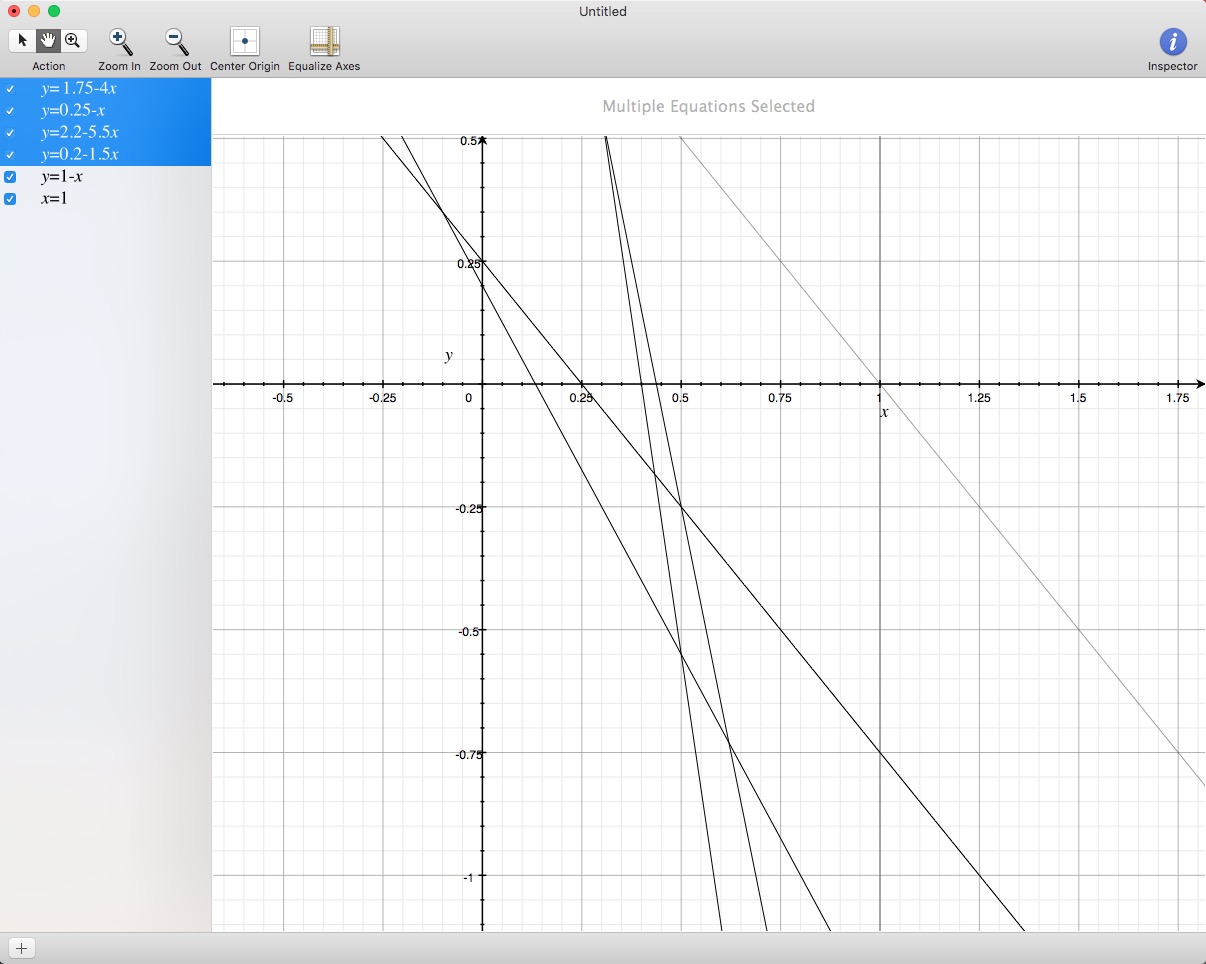
序
数学是基础科学,我觉得我所受到的教育对我等懒人不出效果,但足够唤醒我了。
还是要先学应用,在学基础科学,学以致用嘛。
三等讲题,列举一堆看起来还不错的例子。
二等讲题,用自己的思路来描述“定理/理论”。
一等讲题,讲自己的思路是怎么来的,例如受什么启发,讲自己的有什么思维定式。
共勉。