http://www.usaco.org/index.php?page=viewproblem2&cpid=138
首先第一反应是可以做n2的dp,但是总有种预感是会有更优化的解法,想了想优化dp的迭代过程又没有结果。这时我有种感觉是这题可以用队列做,找单调性。
好的答案来了
设dp[i]是放完前i本书以后 书架的最小高度,显然dp单调递增。
程序从第一本书开始,一本一本的往书架里填塞:
我们用一个双端队列deque记录“最后一层可以摆的最多的书”,每次从尾部push一本书,此时可能会把书从队头挤掉因为一层摆不开,同时也会更新这层的最高height。
我们用一个multiset
例如 有4本书,高度为1 3 3 3,宽度均为1,书架宽度3,放了三本书以后: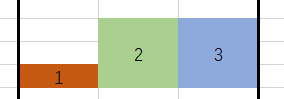
此时deque(书的编号)为[1 2 3],ans为{3, 6, 6, 9},
ans=3 对应于 deque中 3号书后换行
ans=6 对应于 deque中 1号书后换行
ans=6 对应于 deque中 2号书后换行
ans=9 对应于 deque中的1号书、2号书和3号书书后面换行
此时assign dp[3] = ans.min() 理所应当!
--下一次循环
4号书入队,把1号书顶掉,把ans集合的ans=3扔掉。。。(未完待续,很少了,思考一下就清楚了)
Principle:
新来的书放末尾(右侧)
我们保持deque队列自前向后单调递减,“刚放进来的一本书在ans中产生新的height”这种情况,对应于更新比他矮的那些书。
对于在deque中比他还高的那些书如果把他们和新来的这本书它们放在一层,新来的这本书不会更新这层的height,也就不会更新可能的ans,乖乖放进去就是了。因此对于比他矮的会受影响height的书,从队尾把那些书merge,并重新计算被吃掉的书产生的ans。
如图所示队列里有4号书和5号书,当6号书插入的时候,只能对5号书在ans中存的值有影响,对4号书无影响,因此我们此时把5号popback(),直到发现4比6大,再把6号push_back()。
5号被顶替以后,6号在队列里要占据5号的位置,如下图,在计算ans时候,绿色箭头无需计算,因为dp is non-decreasing,在ans中只需要存蓝色箭头的位置。(延申:假如6号特别长,需要把shadow从队首顶掉,那么顶掉时候要更新ans里面的值)
最终放完最后一本,得到答案。
logN而不是1是因为我们要维护一个数据结构能实时得到最小值,增加一个值,删除一个值。睡不着随便发点,明早起来配图!
继续拖个稿,最近的小工程加紧开发中,每天睡觉时间都很紧张,明日再更!
可以练一下:https://leetcode.com/problems/filling-bookcase-shelves/