大意
给定n个数的数组(有正有负),以及一个整数k。
在其中找到不小于k个连续数字的平均值,使之最大。
Analyse1
入手点,先求sum[i]表示前i数的和,则: ans = max{(sum[j]-sum[i])/(j-i)};
于是仔细观察,苦思冥想,得以发现这个是斜率啊!
于是题目变成了,给定若干个点,求两点最大斜率!
引入之前一个答案:https://blog.vrqq.org/archives/80/
怎么想到的呢!看图
We iterate All Node from left to right, 举例,我们走到了点[NOW].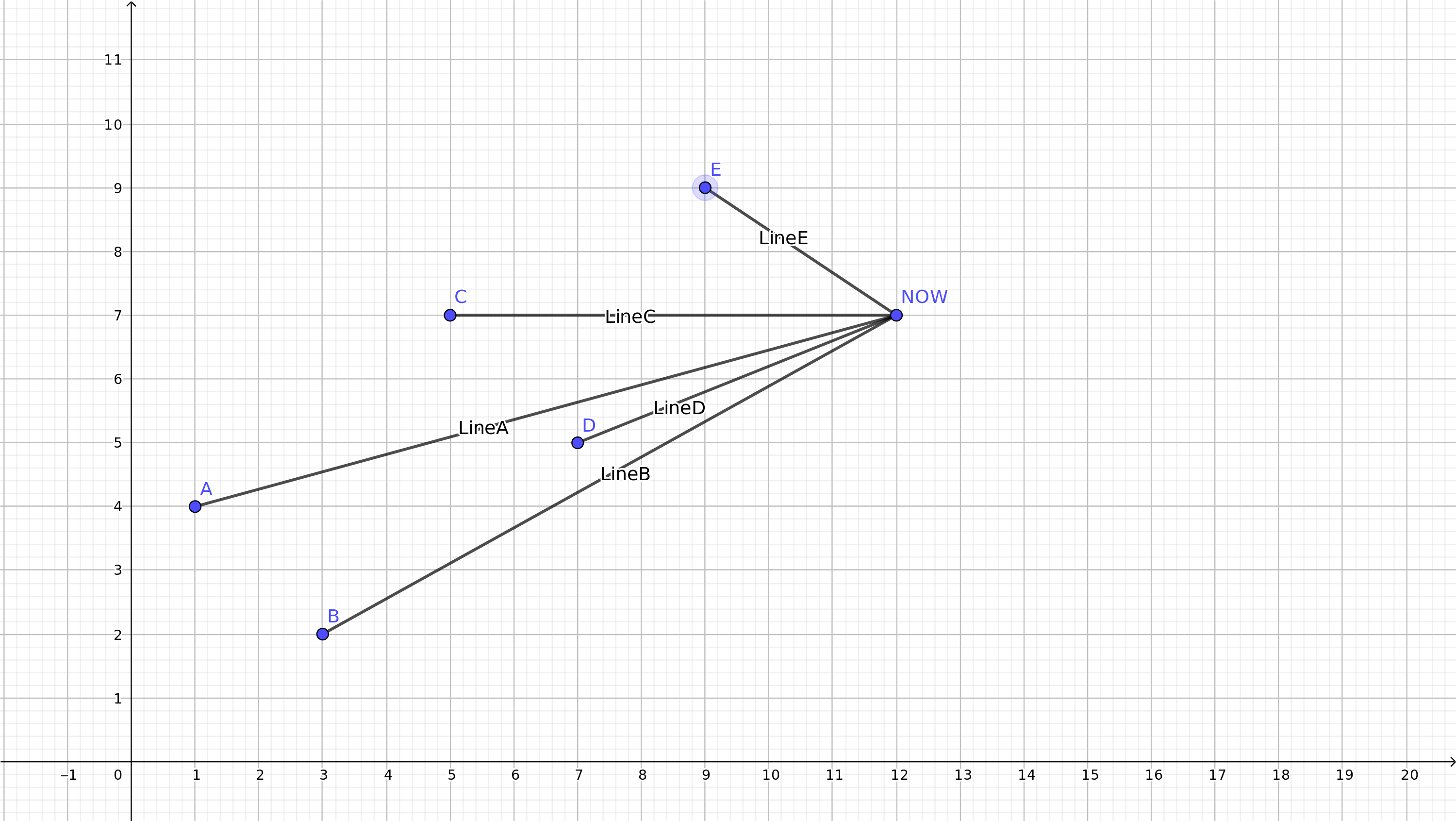
点{A、B、C、D、E}是备选集合,
We can see it, for this Node [now], the best situation is 'B->NOW'.
When we select the node[B], we found that the node on the left side of [B], cannot be better to answer, whether in this round or in the future.
当我们选择B点以后,我们发现,B点左边的点,均不可能比B点更优秀!(IMPORTANT)
选了B->NOW以后,全局ans必然不会低于B->NOW这条线,也就是说:永远不会使用B点左侧的点再次更新全局ans。
于是我们删除点A,得到下图。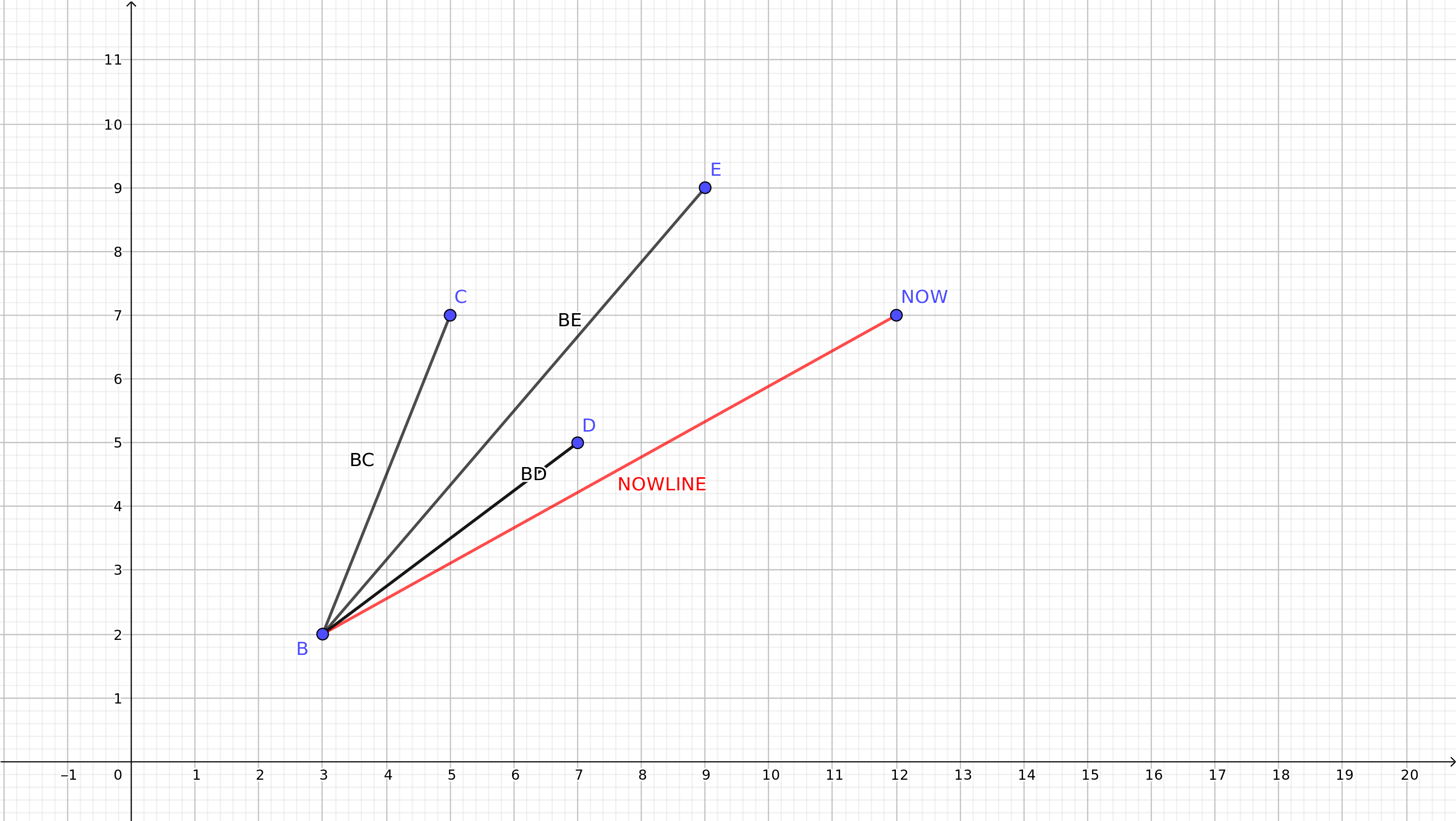
接下来我们反着利用上面那条原则。
连接BC,BD,BE,so we got a new guideline:
当前解为NEWLINE,我们发现集合中,B右侧的所有点,到B的连线,都比NEWLINE优秀。也就是说,“在now这一轮选择了B”也意味着BC、BD、BE的斜率都比NEWLINE大。
在仔细思考为何删掉点A,因为AB的斜率小于NEWLINE,所以A点才没用了。
就是说,如图,假设以后多了一个点FUTURE,FUTURE选定的最小斜率是点[D]。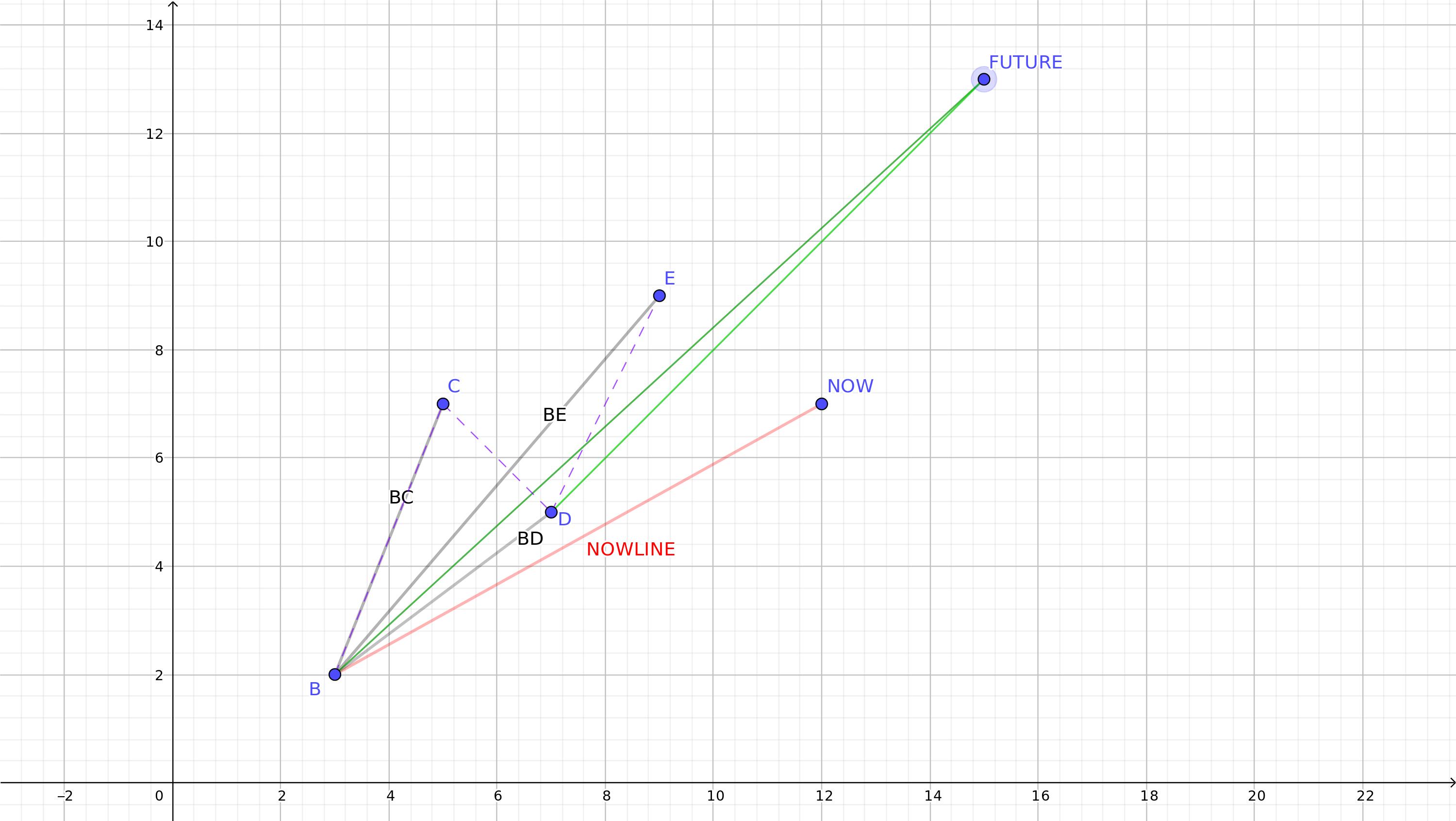
So, BD's slope is smaller than D-FUTURE, so we should remove node B and C.
OK, why D? base on the guideline above, node D is the node we want to select, we will said that how can we find node D rather C below.
Why not compare with C? Because BD is the only one slope smaller than B-FUTURE, we know if someline over BD, the node B will be lost immediately. And now, the line B-FUTURE over it.
-- A new view --
We always use the first Node of the set to calculate ans.
我们永远使用集合中最左边第一个点来更新ans。
So, we always make the slope in increasing order in the set.
Because if some line over the existing slope in the set, it must over the smallest slope in the set firstly, the smallest slope will be made up by B-D-E.
Then it will keep: when we drop node B, we can find node D directly, rather than compare all node after B.
This is the reason why we needn't compare with C.So the conclusion is : When we insert D at sometime, we remove C from the set.
And by this conclusion, the node in set will be a lower-bound convex hull.
At the end.
Drawing by https://www.geogebra.org/classic#graphing
Attachment: data.zip